ハムレットエンジニアのカンニングノート

Appearance

2022-4-13    PythonReinforcement_LearningAIMachine_TranslateBandit_Algorithm

強化学習を今さら勉強します(バンディッドアルゴリズム)．

バンディッド問題について(当たり確率がわかっている) ​

当たり確率の違うスロットマシーンで一番良いのを選ぶ．

まず，スロットマシーンの当たり確率が下記のようにわかっている場合で選定します．

スロットマシーン/コイン獲得031225
A0.900.050.030.02
B0.800.180.010.01

上表より，期待値を算出する．

E(A)=(0.90∗0+0.05∗3+0.03∗12+0.02∗25)=1.01E(B)=(0.80∗0+0.18∗3+0.01∗12+0.01∗25)=0.91E(A)>1>E(B)

スロットマシーンBは，1枚コインを入れてもリターンが0.91枚しか見込めないので損しかない．

バンディッドアルゴリズム ​

バンディッドアルゴリズムは，当たり確率の調査と期待値の計算を同時にする手順・手法と解釈してます．

調査->集計->期待値->(調査に戻る)

(スロット)
回す->集計->期待値->(回すに戻る)
1st2nd3rd期待値(平均)
A0152
B1000.33
R1R2R3Q3

上表の期待値を示すと，下式のようになる．

Q3=(R1+R2+R3)3=(0+1+5)3=2Q2=(R1+R2)3−1=(0+1)2=0.5

Q2を利用すると，Q3は下式のようになる．

(2)Q2=(3−1)Q2=R1+R2Q3=((3−1)Q2+R3)3

Q3をQnとすると，下式のようになります．

Qn=((n−1)Qn−1+Rn)n=(1−1n)Qn−1+1nRn=Qn−1+1n(Rn−Qn−1)

上式より，下記のことが言える．

  • n回目の期待値は「n-1回目の期待値とn回目の報酬」で決定する
  • n回目の期待値がn-1回目の期待値で導出できるため，コードも逐次更新で記述できる
  • (1/n)より回数を重ねるたびに，期待値の更新幅が小さくなる．

調査方法について ​

調査->集計->期待値->(調査に戻る)

(スロット)
回す->集計->期待値->(回すに戻る)

調査をするのはいいが，どのような調査方法でやるのか？

下記の方法が考えられる．

  • ランダムに調査する．(コイントスでA or Bのどちらを回すか決める)
  • 今のところ，一番いいものから調査する(AがよければAを回す，次に調査する時にBがよければBを回す)

上記のことはをそれぞれ「探索」と「活用」と呼ぶ．

  • 探索：ランダムに調査する．(コイントスでA or Bのどちらを回すか決める)
  • 活用：今のところ，一番いいものから調査する(AがよければAを回す，次に調査する時にBがよければBを回す)

強化学習のアルゴリズムは**「探索」と「活用」のバランス**をどうするかを，設定している．

例：ε-geedy法：調査のうち，ε(10%)を「探索」，残り(90%)を「活用」で設定する．

1st(探索)2nd~10th(活用)11th(探索)12nd~20th(活用)21th(探索)22nd~30th(活用)
A(ランダム)A(A>B)B(ランダム)B(A<B)A(ランダム)B(A<B)

報酬(R)と価値(Q)の記述 ​

下式を実装している．

Qn=(Rn+Rn−1+...+R1)nQn=Qn−1+1n(Rn−Qn−1)
python
import numpy as np

# naive implementation
np.random.seed(0)
rs = 
for n in range(1, 10):
    r = np.random.rand()
    rs.append(r)
    q = sum(rs) / n
    print(q)

print('---')

# incremental implementation
np.random.seed(0)
q = 0
for n in range(1, 10):
    r = np.random.rand()
    q = q + (r - q) / n
    print(q)

# 0.5488135039273248
# 0.6320014351498722
# 0.6222554154571295

バンディット問題の実装 ​

ε-geedy法で実装します．

バンディット(スロットマシーンの設定) ​

  • Bandit_class
    • arms：選択肢:ここではスロットマシーンの台数
    • rates:当たり確率(初期値なのでランダム)
python
import numpy as np
import matplotlib.pyplot as plt

# 選択肢(スロットマシーン)の設定
class Bandit:
    def __init__(self, arms=10):
        # arm:選択肢
        self.arms = arms # ここではスロットマシーンの台数
        # rates:当たり確率(ランダムで設定し固定)
        self.rates = np.random.rand(arms) #0~1を10セット
    # arm番目のスロットマシーンをプレイ
    def play(self, arm):
        rate = self.rates[arm] # arm番目のスロットの確率
        reward = rate > np.random.rand() # 確率が乱数より上の時,報酬あり
        return int(reward)
python
bandit = Bandit()

for i in range(3):
    # 0番目のスロットを回す
    print(bandit.play(0))

Agent(CPUプレイヤー)の設定 ​

過去のスロットマシーンの調査から何番目を回すか選択する．

  • Agent_class
    • action_size:スロットマシーンの選択肢数
    • epsilon：探索の割合
    • rs: 各プレイごとの価値(Q)
    • ns: 各プレイごとのプレイ回数[1,1,...,1]
  • def get_action(self):
    • 活用と探索の選択はランダム乱数(一様分布)<epsilonで管理
    • 上記でおおよそ，活用:探索=9:1となる
    • 探索:過去の価値(Q)からランダムに選択
    • 活用:過去の価値(Q)の最大値

self.qs[a] += (r - self.qs[a]) / self.ns[a]

Qn=Qn−1+1/n(Rn−Qn−1)
python
# Agent(CPUプレイヤー)の設定
class Agent:
    def __init__(self, epsilon, action_size=10):
        self.epsilon = epsilon # 探索の割合
        self.qs = np.zeros(action_size) # 各スロットマシーンの価値(Q)のリスト [0,...,0]
        self.ns = np.zeros(action_size) # 各スロットマシーンの「探索or活用」回数のリスト(1のリスト) [0,...,0]
    # 更新(リストに格納)
    def update(self, action, reward):
        a, r = action, reward
        self.ns[a] += 1 # 各スロットマシーンの「探索or活用」回数をカウント
        self.qs[a] += (r - self.qs[a]) / self.ns[a] # Q_{n-1}による各スロットマシーンの報酬更新
        
    # Agent(CPUプレイヤー)のプレイ
    def get_action(self):
        # ランダム乱数でepsilon以下の時
        if np.random.rand() < self.epsilon:
            return np.random.randint(0, len(self.qs)) # ランダムに選択(探索)
        return np.argmax(self.qs) # 最大値を選択(活用)

バンディット問題の実行 ​

  • main
    • steps: 1探索or活用_arms回プレイをstep回する
    • epsilon：探索の割合
    • sum_r:報酬合計
    • total_rewards:報酬合計リスト
    • rates:平均報酬リスト
python
if __name__ == '__main__':
    # 1探索or活用_10回プレイを1000回する
    steps = 1000
    epsilon = 0.1

    bandit = Bandit()
    agent = Agent(epsilon)
    sum_r = 0
    total_rewards = 
    rates = 
    
    for step in range(steps):
        action = agent.get_action() # 探索or活用より何番目を回すか選択
        reward = bandit.play(action) # action番目をプレイ
        agent.update(action, reward) # action番目のSM報酬を更新
        sum_r += reward # 報酬合計を更新
        total_rewards.append(sum_r) # 報酬合計をリストに格納
        rates.append(sum_r / (step+1)) # 平均報酬をリストに格納

    print(sum_r)
    # 各ステップの報酬合計をプロット
    plt.ylabel('Total reward')
    plt.xlabel('Steps')
    plt.plot(total_rewards)
    plt.show()
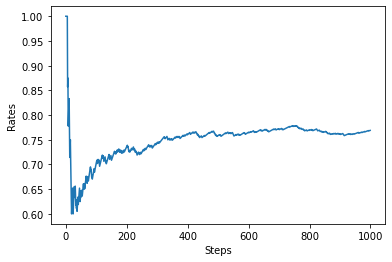
    # 各ステップの平均報酬をプロット
    plt.ylabel('Rates')
    plt.xlabel('Steps')
    plt.plot(rates)
    plt.show()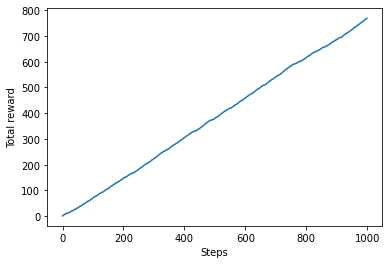

png

png

アルゴリズムの性質 ​

下記のコードでは，steps回の探索・活用をrun回分_ε-geedy法で実行しています．

python
import numpy as np
import matplotlib.pyplot as plt
# from bandit import Bandit, Agent

runs = 2000
steps = 1000
epsilon = 0.1
all_rates = np.zeros((runs, steps))  # (2000, 1000)

for run in range(runs):
    bandit = Bandit()
    agent = Agent(epsilon)
    sum_r = 0
    rates = 

    for step in range(steps):
        action = agent.get_action()
        reward = bandit.play(action)
        agent.update(action, reward)
        sum_r += reward
        rates.append(sum_r / (step+1))

    all_rates[run] = rates

avg_rates = np.average(all_rates, axis=0)

plt.ylabel('Rates')
plt.xlabel('Steps')
plt.plot(avg_rates)
plt.show()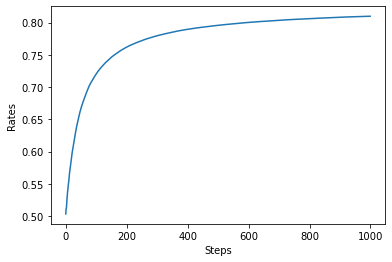

png

そして，上記のコードよりepsilonを0.1, 0.3, 0.01に変化させてプロットします．

python
import numpy as np
import matplotlib.pyplot as plt
# from bandit import Bandit, Agent

runs = 2000
steps = 1000
epsilon = 0.1
all_rates = np.zeros((runs, steps))  # (2000, 1000)

for epsilon in [0.1, 0.3, 0.01]:
    for run in range(runs):
        bandit = Bandit()
        agent = Agent(epsilon)
        sum_r = 0
        rates = 

        for step in range(steps):
            action = agent.get_action()
            reward = bandit.play(action)
            agent.update(action, reward)
            sum_r += reward
            rates.append(sum_r / (step+1))

        all_rates[run] = rates

    avg_rates = np.average(all_rates, axis=0)

    plt.ylabel('Rates')
    plt.xlabel('Steps')
    plt.plot(avg_rates)
plt.legend(["0.1", "0.3", "0.01"])
plt.show()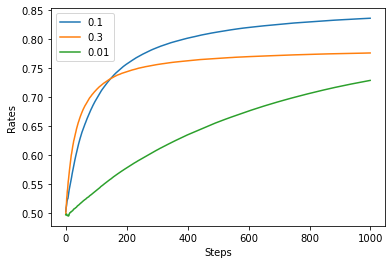

png

非定常問題 ​

前述のバンディット問題は，下記のコードより当たり確率は固定でした．

python
# 選択肢(スロットマシーン)の設定
class Bandit:
    def __init__(self, arms=10):
        # (省略)
        # rates:当たり確率(ランダムで設定し固定)
        self.rates = np.random.rand(arms) #0~1を10セット

これより，スロットマシーンの設定を少しでもいじられたら，また1000回プレイしないといけません．

これでは，当たり確率が変動する場合を考慮した非定常バンディット問題を実装します．

非定常バンディット問題については，下記の2つを考慮します．

  • 当たり確率の変動：当たり確率をいじられた時を考慮する

  • データの重み：更新されたデータを重く見るために，最新版のデータを重視する

当たり確率の変動 ​

当たり確率をいじられた時を考慮する

python
class NonStatBandit:
    def __init__(self, arms=10):
        self.arms = arms
        self.rates = np.random.rand(arms)

    def play(self, arm):
        rate = self.rates[arm]
        reward = rate > np.random.rand()
        self.rates += 0.1 * np.random.randn(self.arms)  # 乱数で当たり確率を変動させる
        return int(reward)
python

データの重み ​

更新されたデータを重く見るために，最新版のデータを重視する

python
class AlphaAgent:
    def __init__(self, epsilon, alpha, actions=10):
        self.epsilon = epsilon
        self.qs = np.zeros(actions)
        self.alpha = alpha

    def update(self, action, reward):
        a, r = action, reward
        self.qs[a] += (r - self.qs[a]) * self.alpha  # 更新データを係数より重視

    def get_action(self):
        if np.random.rand() < self.epsilon:
            return np.random.randint(0, len(self.qs))
        return np.argmax(self.qs)

非定常問題の実行 ​

  • sample average:定常問題
  • alpha const update:非定常問題
python
runs = 2000
steps = 1000
epsilon = 0.1
alpha = 0.8
agent_types = ['sample average', 'alpha const update']
results = {}

for agent_type in agent_types:
    all_rates = np.zeros((runs, steps))  # (2000, 1000)

    for run in range(runs):
        if agent_type == 'sample average':
            agent = Agent(epsilon)
        else:
            agent = AlphaAgent(epsilon, alpha)

        bandit = NonStatBandit()
        sum_r = 0
        rates = 

        for step in range(steps):
            action = agent.get_action()
            reward = bandit.play(action)
            agent.update(action, reward)
            sum_r += reward
            rates.append(sum_r / (step+1))

        all_rates[run] = rates

    avg_rates = np.average(all_rates, axis=0)
    results[agent_type] = avg_rates

# plot
plt.figure()
plt.ylabel('Average Rates')
plt.xlabel('Steps')
for key, avg_rates in results.items():
    plt.plot(avg_rates, label=key)
plt.legend()
plt.show()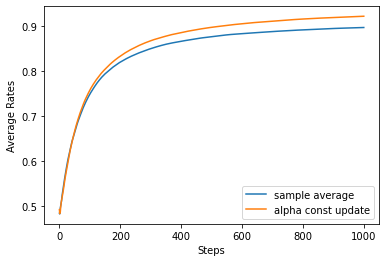

png

まとめ ​

強化学習を今さら勉強しました(バンディッドアルゴリズム)．

MIT Licensed | Copyright © 2021-2022 ハムレットエンジニアのカンニングノート
Powered by VitePress - 1.6.1 Theme by Vitepress-blog